¡Demasiados puntos!
Hace un tiempo tuve que leer desde Python unos archivos hechos en AutoCad. Básicamente tuve que extraer la geometría de distintos polígonos para luego continuar mi análisis. Sin embargo, no sospechaba la cantidad de puntos que podían estar contenidos en cada uno de los polígonos. Claramente para un amante del detalle, como yo, era genial tener una información tan precisa. Lamentablemente, el número de puntos era tan grande que mis rutinas se demoraban muchísimo más de lo que podía esperar.
Si uno observaba la geometría de los polígonos, fácilmente se podía dar cuenta que muchos puntos podrían ser simplificados a través de una recta. Obviamente sería una aproximacion, pero el resultado final no afectaría a mi modelización completa. Para ejemplificar este problema, sin embargo, voy a utilizar la geografía de los países del mundo.

Los 247 países del mundo. Fuente: Natural Earth
Ideas al aire
La primera idea que tuve para solucionar este problema fue determinar los ángulos interiores entre cada segmento del polígono e ir eliminando los puntos que estuvieran asociados a un ángulo mayor a un umbral previamente definido. Sin embargo, esta idea tenía el problema de que si eliminaba un punto cambiaría el ángulo de los dos puntos contiguos, lo cual requeriría estar revisando la nueva configuración repetidamente. No es que suene muy difícil, pero antes de implementarlo hay que pensarlo bien.
Algo más serio
Luego de pensar un poco, me pregunté si existía alguna forma mejor para resolver este problema. Y sí la hay, corresponde al algoritmo Ramer-Douglas-Peucker. El algoritmo consiste en reducir de manera recursiva los puntos que caen dentro de un umbral de distancia. Los pasos son los siguientes:
def RDP(xy, epsilon):
# 1. Considera la recta L definida por el punto inicial y final de xy
L = [xy[0], xy[-1]]
# 2. Si no hay puntos entre medio del primero y el último, finaliza la
# función retornando los dos puntos.
if len(xy) == 2:
return xy
# 3. Si hay más puntos, calcula la distancia de cada punto interior con la
# recta L (distancia punto-recta) e identifica el punto
# que tenga la mayor distancia, d_max.
else:
d_max = 0.
for i in xrange(len(xy)-2):
d = distancia_punto_recta(xy[i+1], L)
if d > d_max:
index = i
d_max = d
# 4. Si d_max es menor que epsilon, se finaliza la función retornando sólo
# los puntos inicial y final (es decir, descartamos todos los puntos
# interiores).
if d_max <= epsilon:
return [xy[i] for i in [0, -1]]
# 5. En cambio, si d_max es mayor que epsilon, el set de puntos se divide
# en dos: uno desde el punto inicial hasta el asociado a d_max y otro
# desde el mismo punto hasta el final. Luego se hacen dos llamados a
# RDP, uno con cada sub set recién definidos. Finalizamos la función
# juntando el resultado de cada llamado a RDP y entregando eso como
# salida final.
else:
sub_set_1 = RDP(xy[:index+1], epsilon)
sub_set_2 = RDP(xy[index:], epsilon)
return sub_set_1.extend(sub_set_2[1:])
Primero que todo quiero decir que el algoritmo me ha parecido genial. Cuando lo entiendes y ves lo simple que es, pero al mismo tiempo te preguntas cómo no se te ocurrió antes, te das cuenta lo bien que está hecho. Una demostración gráfica del algoritmo, paso a paso, se puede ver en esta animación que está disponible en el artículo de Wikipedia.
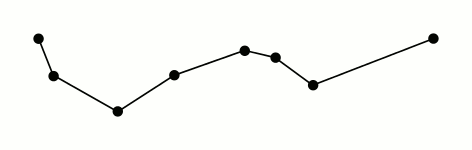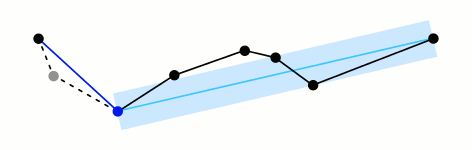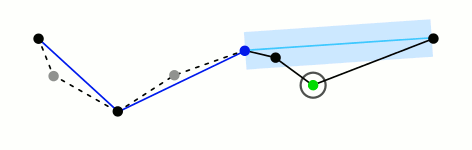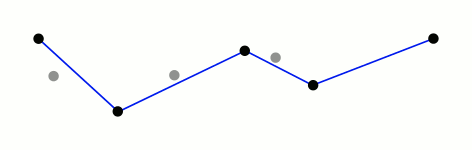
Animación del algoritmo Ramer-Douglas-Peucker. Figura hecha por Mysid, distribuída bajo la licencia CC BY-SA 3.0
Implementación en Python
En este caso el pseudo código quedó practicamente listo para usar en Python. Sólo faltaría definir la función distancia_punto_recta. Sin embargo, deseo dejar una versión iterativa del código en vez de la recursiva. En otra entrada discutiré sobre la transformación de algoritmos recursivos a iterativos, de momento sólo dejaré este código que compartí con la librería rdp que pueden instalar utilizando el comando pip install rdp.
# Librerías necesarias
from math import sqrt
import numpy as np
# Distancia punto-recta
def PointLineDistance(point, start, end):
if np.all(np.equal(start, end)) :
return np.linalg.norm(point - start)
n = abs((end[0] - start[0]) * (start[1] - point[1]) - (start[0] - point[0]) * (end[1] - start[1]))
d = sqrt((end[0] - start[0]) * (end[0] - start[0]) + (end[1] - start[1]) * (end[1] - start[1]))
return n/d
# Algoritmo de Ramer-Douglas-Peucker iterativo (local)
def _RamerDouglasPeucker(points, startIndex, lastIndex, epsilon):
stk = []
stk.append([startIndex, lastIndex])
globalStartIndex = startIndex
bitArray = np.ones(lastIndex-startIndex+1, dtype=bool)
while len(stk) > 0:
startIndex = stk[-1][0]
lastIndex = stk[-1][1]
stk.pop()
dmax = 0.
index = startIndex
for i in xrange(index+1, lastIndex):
if bitArray[i - globalStartIndex]:
d = PointLineDistance(points[i], points[startIndex], points[lastIndex])
if d > dmax:
index = i
dmax = d
if dmax > epsilon:
stk.append([startIndex, index])
stk.append([index, lastIndex])
else:
for i in xrange(startIndex + 1, lastIndex):
bitArray[i - globalStartIndex] = False
return bitArray
# Algoritmo de Ramer-Douglas-Peucker iterativo
def RamerDouglasPeucker(points, epsilon):
bitArray = _RamerDouglasPeucker(points, 0, len(points)-1, epsilon)
resList = []
for i in xrange(len(points)):
if bitArray[i]:
resList.append(points[i])
return np.array(resList)
La ventaja de este código es que trabaja con arreglos de NumPy, además que acepta arreglos en que el primer y el último punto sean el mismo (hay gente que le gusta definir así los polígonos...). Además nos evitamos los problemas de memoria que puede generar un código recursivo. A continuación dejo algunos resultados que muestran la efectividad del algoritmo.
